Welcome to this informative topic on the “Area of Square.” Squares are one of the most fundamental and fascinating shapes in mathematics and geometry. With their unique properties and significance in various fields, understanding their area is essential for students, professionals, and enthusiasts alike. In this article, we will delve into the depths of squares, exploring their characteristics, calculations, and practical applications. So, let’s embark on this geometric journey and discover the captivating world of squares!
Before we begin our exploration, let’s understand the definition of a square and its key properties.
A square is a regular quadrilateral with four equal sides and four right angles. Its sides are congruent, and its angles are each 90 degrees. Due to these unique characteristics, squares possess symmetry and uniformity, making them a fundamental shape in geometry.
There are multiple methods related to its area calculation:
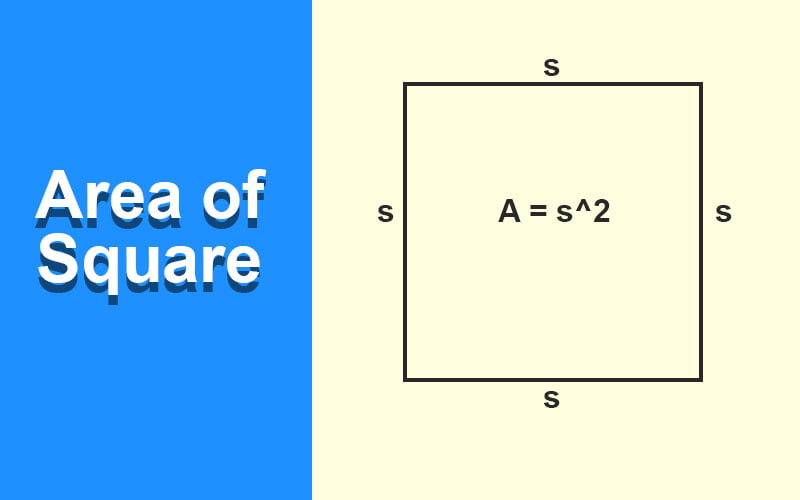
Since all the sides are equal, the simplest way to calculate the area of a square is by squaring the length of one of its sides. If the side length is “s,” the area “A” is given by the formula:
A = s^2
Another approach to finding the area of a square involves knowing the length of its diagonal, “d.” The area can be determined using the diagonal length with the following formula:
A = (d^2) / 2
The area of a square can also be determined using its perimeter, “P,” and the side length, “s.” The formula to calculate the area is:
A = P^2 / 16
A square’s area can be found by knowing the radius of its circumscribed circle, “r.” The formula for the area in this case is:
A = 2 * r^2
The area of a square finds applications in various fields, particularly construction to art and beyond.
Specifically in architecture, knowing the area of a square is crucial for calculating the space it occupies in a building’s floor plan. It helps architects design spaces efficiently and allocate resources effectively.
In land surveying, squares are used to divide plots into uniform sections for accurate measurement. Calculating the area of these squares aids in determining land value and taxation.
Squares play a significant role in art and design, with artists often using them to create balanced compositions. Thus understanding the area helps artists plan their work and use space harmoniously.
In engineering and manufacturing, squares are employed in various designs and calculations. Knowing the area is essential for manufacturing processes and material estimation.
A: The formula to find the area of a square is A = s^2, where “s” represents the length of one side.
A: Yes, the area of a square can be determined using its perimeter with the formula A = P^2 / 16.
A: A square exhibits four lines of symmetry, dividing it into four congruent parts.
A: The key properties of a square include equal side lengths, right angles, equal diagonals, and four lines of symmetry.
A: In architecture, knowing the area of a square is crucial for efficient space planning and resource allocation.
A: Squares are commonly used in art and design to create balanced and harmonious compositions.
In conclusion, the area of a square is a fundamental concept in geometry with practical applications across various domains. Understanding its properties and calculations not only enhances our knowledge of geometry but also aids us in diverse fields, from architecture to art and beyond. So, the next time you encounter a square, take a moment to appreciate its unique properties and the mathematical wonders it holds within its symmetrical boundaries.
Recommended other topics: Drone Camera-Capturing the Skies from a New Perspective










© InfoDoot. All Rights Reserved.