Area of Trapezium: Understanding the Concepts and Calculations

Introduction

Welcome to our comprehensive guide on the area of a trapezium! In this article, we will explore the intricacies of this fascinating geometric shape and delve into its mathematical properties. Whether you’re a student seeking to understand trapeziums for academic purposes or simply curious about the mathematics behind them, we’ve got you covered. So, let’s embark on this journey of discovery!

Area of Trapezium: The Basics

A trapezium, also known as a trapezoid in North America, is a quadrilateral with one pair of parallel sides. To understand its area, we need to examine its unique characteristics and the formula used for calculation.

Characteristics of a Trapezium:

A trapezium is defined by the following properties:

• It has four sides.
• Only one pair of opposite sides is parallel.
• The non-parallel sides may or may not be of equal length.
• It is not necessary for the angles between the sides to be right angles.

Formula for Calculating the Area:

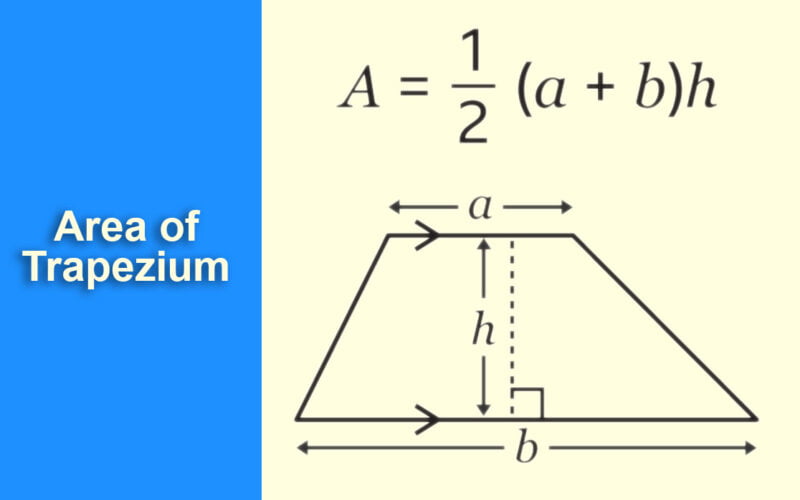
The area of a trapezium can be calculated using the following formula:

Area = (1/2) × (sum of parallel sides) × (distance between parallel sides)

Calculating the Area: Step-by-Step Guide

Let’s take you through the step-by-step process of calculating the area of a trapezium.

Step 1: Identify the Parallel Sides and Height

Before we begin, identify the two parallel sides of the trapezium and the distance between them, which is referred to as the “height” of the trapezium.

Step 2: Add the Lengths of Parallel Sides

Take the sum of the lengths of the parallel sides and write it down.

Step 3: Multiply by Half

Multiply the sum obtained in Step 2 by half (1/2).

Step 4: Multiply by the Height

Now, multiply the result from Step 3 by the height of the trapezium. This will give you the area of the trapezium in square units.

Step 5: Add Units

Don’t forget to include the appropriate unit (e.g., square centimeters, square inches) to represent the area.

Examples: Understanding with Practical Scenarios

To grasp the concept better, let’s work through a couple of examples that demonstrate how to calculate the area of a trapezium.

Example 1:

Consider a trapezium with parallel sides measuring 8 centimeters and 12 centimeters and a height of 6 centimeters.

Area = (1/2) × (8 + 12) × 6 = 60 square centimeters

Example 2:

Now, let’s examine a trapezium with parallel sides measuring 15 inches and 20 inches, and a height of 10 inches.

Area = (1/2) × (15 + 20) × 10 = 175 square inches

Applications of Trapeziums in Real Life

Trapeziums might seem like abstract geometric shapes, but they have several real-life applications. Understanding the concept of the area of a trapezium can prove beneficial in various fields:

• Architecture and Construction: Architects and construction professionals often encounter trapezoidal areas when designing roofs, windows, or inclined surfaces.
• Landscaping: In landscaping projects, calculating the area of trapezoidal gardens or lawns is essential for determining the required materials and costs.
• Surveying and Mapping: Trapeziums are used in surveying land, especially when the boundaries are irregular.
• Engineering: Engineers frequently use trapezoidal areas in designing roads, bridges, and various structures.

FAQs

Q: What is the difference between a trapezium and a trapezoid?

A: A trapezium in the UK and other countries refers to a quadrilateral with one pair of parallel sides. In North America, a trapezoid is defined as a quadrilateral with at least one pair of parallel sides.

Q: Are all trapeziums symmetrical?

A: No, not all trapeziums are symmetrical. Trapeziums can have non-parallel sides of different lengths, resulting in asymmetry.

Q: Can a trapezium have more than one right angle?

A: Yes, a trapezium can have more than one right angle, but it must have one pair of parallel sides.

Q: How do trapeziums differ from parallelograms?

A: The key difference is that parallelograms have both pairs of opposite sides parallel, whereas trapeziums have only one pair of parallel sides.

Q: Can a trapezium have equal-length sides?

A: Yes, a trapezium can have equal-length sides, known as an isosceles trapezium.

Q: Why is it essential to calculate the area of a trapezium accurately?

A: Accurate calculations of the area of a trapezium are crucial in various fields, such as construction, architecture, and engineering, as it helps in determining quantities of materials required and associated costs.

Conclusion

In conclusion, understanding the area of a trapezium is an essential aspect of geometry with practical applications in diverse fields. By following the step-by-step guide and grasping the concept’s intricacies, you can confidently calculate the area of any trapezium you encounter. Whether you’re a student, professional, or simply curious, we hope this article has enriched your knowledge and provided valuable insights into the fascinating world of trapeziums.

Recommended other topics: Area of Square-Understanding the Fundamentals